Wszystko... jest liczbą

Fraktal – słowo to wywodzi się od łacińskiego fractus – złamany, cząstkowy, ułamkowy. Pojęcie fraktala wprowadził do nauki w latach 70. francuski matematyk Benoît B. Mandelbrot. Słowem tym bywają określane różnorodne obiekty; autorzy piszący o fraktalach często unikają podawania dokładnej definicji. Fraktale definiowane są na różne sposoby i zazwyczaj są to definicje dosyć skomplikowane. Najczęściej jednak mówi się o obiektach cechujących się samopodobieństwem, tzn. że części obiektu są pomniejszoną, dokładną lub przybliżoną kopią całości. Ich strukturę trudno opisać za pomocą tradycyjnej geometrii, ale bardzo często przepis, według którego są budowane, jest bardzo prosty. Wiele obiektów mających cechy fraktali znanych było dużo wcześniej, nim wprowadzono to pojęcie.

W naturalny sposób mówimy, że prosta jest obiektem jednowymiarowym, płaszczyzna dwuwymiarowym, zwykła przestrzeń zaś trójwymiarowym. Jest to zgodne z intuicyjnym podejściem do pojęcia wymiaru jako minimalnej liczby parametrów potrzebnych do opisania jakiegoś zbioru. Na bazie tej prostej intuicji matematycy operują co najmniej kilkoma różnymi definicjami wymiaru. W przypadku obiektów fraktalnych (np. trójkąta Sierpińskiego z nieskończoną ilością dziur) zastosowanie różnych definicji wymiaru daje różne rezultaty.

Najprostsza do zrozumienia jest następująca sytuacja: zliczane są kostki, czyli pudełka, którymi pokrywa się badaną figurę. W przejściu granicznym z rozmiarem kostki zmierzającym do zera otrzymujemy wymiar obiektu. W przypadku obiektów o łatwym do opisania przepisie wygodniej jest jednak zastosować wymiar samopodobieństwa. Jeśli mierzony obiekt zawiera N samopodobnych kopii wielkości s, to wymiar D zdefiniowany jest równaniem: Ns^D=1. 

Liczby wpisane w kółka na tablicy tworzą trójkąt Pascala. Powstaje on w ten sposób, że każda znajdująca się w nim liczba jest sumą dwóch liczb znajdujących się bezpośrednio nad nią. Jednocześnie każdy n-ty wiersz zawiera współczynniki rozwinięcia dwumianu Newtona (a+b)ⁿ. Liczby w trójkącie Pascala mają wiele ciekawych właściwości, np. suma liczb w każdym wierszu daje w wyniku kolejne potęgi liczby 2.

Za pomocą magnetycznych krążków należy zasłonić na tablicy wszystkie liczby podzielne przez 2. Zasłonięte liczby tworzą pewną strukturę strukturę geometryczną przypominającą Trójkąt Sierpińskiego. Doświadczenie można powtórzyć, zasłaniając liczby podzielne przez 3, 5 i inne liczby. Również w tym przypadku powstają struktury geometryczne o charakterze fraktalnym.

Trójkąt Sierpińskiego otrzymuje się wg następującego przepisu: w trójkącie równobocznym łączy się środki boków, dzieląc go w ten sposób na cztery mniejsze trójkąty, a następnie usuwa się środkowy trójkąt. Operację powtarza się w trzech pozostałych trójkątach, dzieląc każdy z nich na cztery mniejsze trójkąty, usuwając środkowy, a dla pozostałych po raz kolejny powtarzając opisane czynności. Trójkąt Sierpińskiego to jeden z najwcześniej poznanych obiektów mających cechy fraktala. Został opisany w 1915 roku przez polskiego matematyka Wacława Sierpińskiego (1882-1969).

Należy przenieść stos krążków z pierwszego pręta na ostatni, zachowując kolejność od największego do najmniejszego i przestrzegając następujących reguł:

1.      wolno przenosić tylko jeden krążek z wierzchu stosu, nie wolno kłaść większego krążka na mniejszym,

2.      wolno wykorzystywać środkowy pręt do chwilowego odkładania krążków.

Wieże Hanoi są przykładem problemu, którego złożoność bardzo szybko rośnie wraz ze wzrostem liczby krążków. Minimalną liczbę ruchów potrzebnych do przeniesienia n krążków można obliczyć ze wzoru N=2n - 1. Dla sześciu krążków wynosi ona 63.

Zagadkę wież Hanoi wymyślił w 1883 roku matematyk Édouard Lucas (1842-1991). Sprzedawał ją jako zabawkę w wersji z ośmioma krążkami. Prawdopodobnie to sam Lucas był autorem „tybetańskiej legendy" rzekomo wyjaśniającej pochodzenie łamigłówki.

W świątyni Brahmy w Tybecie znajdują się podobne wieże, na które nałożono 64 krążki ze szczerego złota. Dzień i noc mnisi przekładają krążki, a gdy zakończą swoją pracę nastąpi koniec świata. Jednak nie ma powodu do obaw – zakładając, że wykonanie jednego ruchu trwa jedną sekundę, praca zajmie im jeszcze ok. 584 tryliony lat.

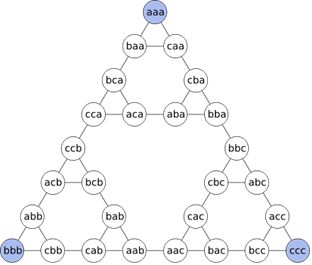
Jaki jest związek zagadki Wież z Hanoi z fraktalami? Jeśli przyporządkujemy trzem prętom litery A, B oraz C, to położenie trzech krążków może być opisane za pomocą trzech znaków: np. BBC oznacza, że pierwszy i drugi krążek są na pręcie B, trzeci krążek zaś znajduje  się na pręcie C. Wszystkie dopuszczalne położenia krążków można przedstawić graficznie. Znakomity matematyk i popularyzator nauki Ian Stewart (ur. 1945) zauważył kilka lat temu, że rysunek przedstawiający wszystkie dopuszczalne położenia krążków ma strukturę trójkąta Sierpińskiego.

Na długo przed wprowadzeniem do matematyki słowa fractal znane były obiekty, którym obecnie przypisujemny cechy fraktalne. Należą do nich zbiór Cantora (opisany w 1884 roku przez Georga Cantora), płatek Kocha (opisany w 1904 roku przez Helge von Kocha) oraz trójkąt Sierpińskiego opisany w1915 roku.

Kolejne etapy powstawania tych obiektów można prześledzić używając animacji komputerowej.